Simpson's Rule

Simpson's Rule is a more accurate method of numerical integration than the method illustrated above. Using Simpson's Rule, the integral of a function f between a and b is approximated as

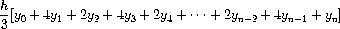
where h = (b − a)/n , for some even integer n , and yₖ = f(a + kh) . (Increasing n increases the accuracy of the approximation.) Define a procedure simpson that takes as arguments f , a , b , and n and returns the value of the integral, computed using Simpson's Rule. Use your procedure to integrate cube between 0 and 1 (with n = 100 and n = 1000), and compare the results to those of the integral procedure shown above.