Three sequences of approximations to the natural logarithm of 2
Use the series
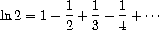
to compute three sequences of approximations to the natural logarithm of
2
, in the same way we did above for
π
. How rapidly do these sequences converge?
There are no comments yet.
Authentication required
You must log in to post a comment.
Login