Правило Симпсона

Правило Симпсона — более точный метод численного интегрирования, чем представленный выше. С помощью правила Симпсона интеграл функции f между a и b приближенно вычисляется в виде

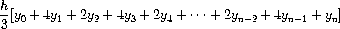
где h = (b − a)/n , для какого - то четного целого числа n , а yₖ = f(a + kh) . (Увеличение n повышает точность приближенного вычисления.) Определите процедуру simpson , которая принимает в качестве аргументов f , a , b и n , и возвращает значение интеграла, вычисленное по правилу Симпсона. С помощью этой процедуры проинтегрируйте cube между 0 и 1 (с n = 100 и n = 1000) и сравните результаты с процедурой integral , приведенной выше.